Diffusion models for time series
On this post I will explore the main findings from the paper “UTSD: Unified Time Series Diffusion Model” and an explanation of the content. For more details here is the link to the paper Link to paper
Summary of Findings from UTSD Paper
The authors of the paper propose a novel architecture, UTSD, for time series analysis. The researchers note the prevalence of time series data in a variety of real world applications. They also point out that data across different domains often have different statistical properties. They posit that this creates a challenge to the generalizability and robustness of time series analysis. In order to address this, the authors propose a unified time series diffusion model. The paper explains that the UTSD model uses a diffusion denoising process, in contrast to autoregressive models, to model the mixture distribution of cross-domain data and generate a prediction sequence for the target domain. The model learns from time series data across a range of domains with the goal of having strong generalization capabilities and robustness to achieve zero-shot inference on unseen domains. UTSD consists of three key designs:
- Condition-denoising architecture
- Reverse noise reduction process in the actual sequence space
- Conditional generation strategy based on improved classifier-free guidance
The paper reports that UTSD outperforms existing foundation models on all data domains. It achieves an average MSE reduction of 14.2%, 20.1%, and 27.6% compared to the existing Moirai, UniTime, and GPT4TS, respectively. The paper also reports that UTSD, when trained from scratch, achieves comparable performance to domain-specific models. In the paper, the authors contend that UTSD shows stable and reliable time series generation which indicates the model’s potential as a foundational model for time series analysis.
Explanation of the Paper
The paper presents a detailed explanation of the UTSD model architecture and its three key design elements. These designs aim to address the challenges of modeling probability distributions across multiple time series domains and generating accurate long-term forecasts.
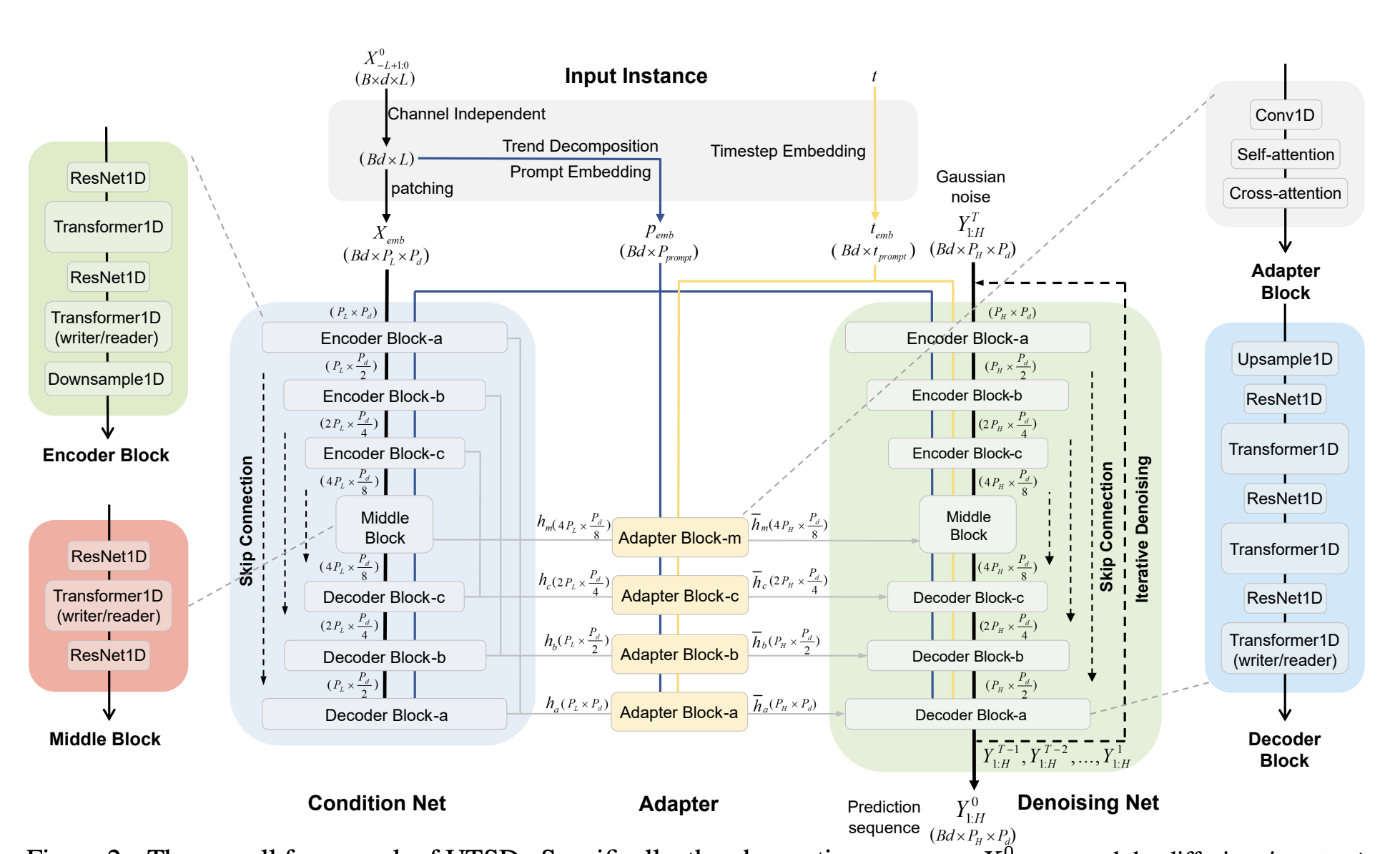
1. Condition-Denoising Architecture
This architecture includes a Condition Net and a Denoising Net. The Condition Net learns multi-scale representations of temporal fluctuation patterns from different time series domains. These representations are then used as conditional variables to guide the Denoising Net in generating the prediction sequence. The paper argues that capturing multi-scale representations is crucial because time series from various domains often exhibit different latent patterns.
2. Reverse Noise Reduction in Actual Sequence Space
UTSD performs the reverse noise reduction process directly in the actual sequence space, unlike traditional diffusion models that operate in a latent space. This design choice is justified by the fact that iterative denoising in the latent space can lead to error accumulation, which is amplified when aligning the latent space back to the actual sequence space.
3. Improved Classifier-Free Guidance
The UTSD model uses an improved classifier-free guidance strategy to ensure strong generalization ability. This strategy leverages the multi-scale representation captured by the Condition Net as a conditional variable to guide the reconstruction of the forecast from Gaussian noise.
Additional Architectural Components
- Transfer-Adapter Module: This module allows for efficient fine-tuning of the pre-trained UTSD model on specific downstream tasks. It transforms the fluctuation patterns learned during pre-training into the latent space of the target domain, enabling the generation of domain-specific time series samples.
- Blocks Implementation: The Condition Net and Denoising Net are built using ResNet1D and Transformer1D modules. The ResNet1D modules handle the embedding of diffusion timesteps and latent representations, while the Transformer1D modules capture dependencies within the observation sequence and leverage historical fluctuation patterns as context for denoising.