Quantization of LLMs
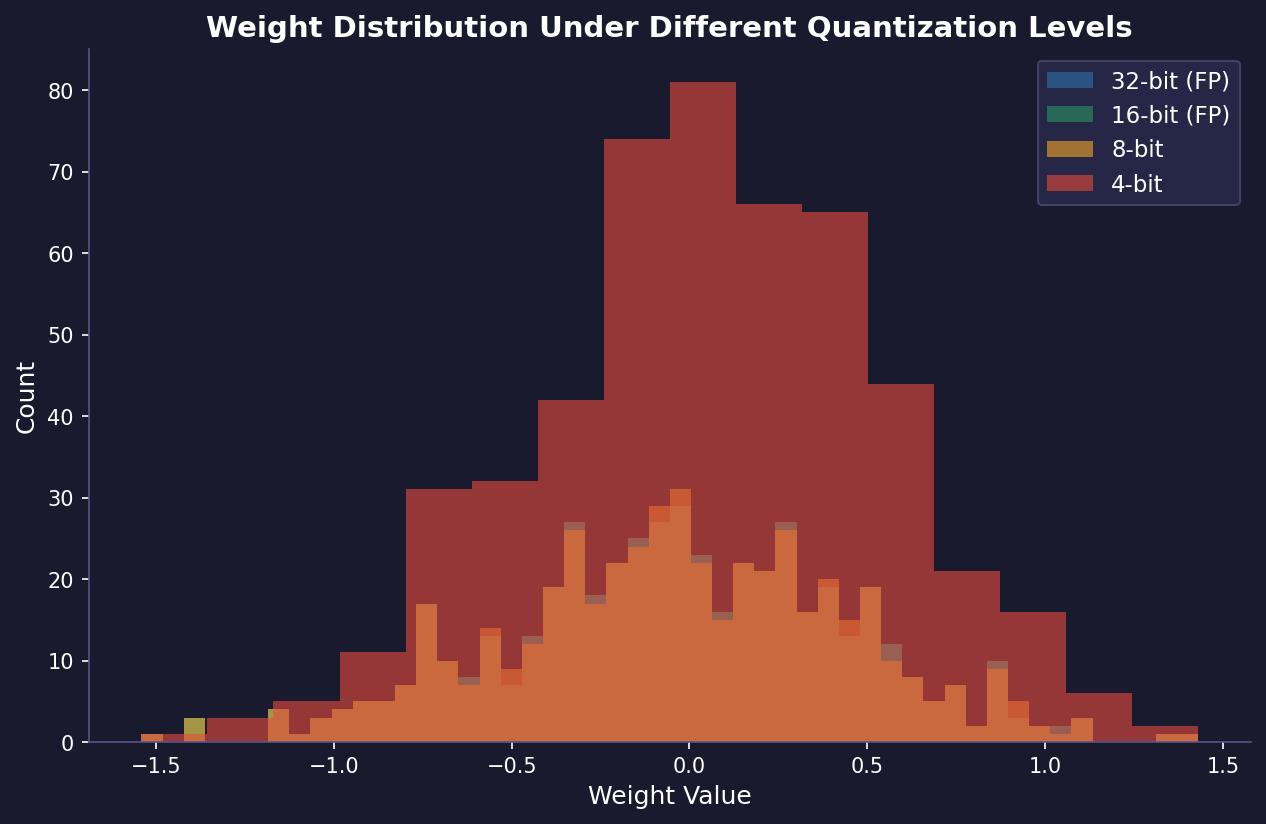
The escalating complexity and scale of large language models (LLMs) have introduced substantial challenges concerning computational demands and resource allocation. These models, often comprising hundreds of billions of parameters, necessitate extensive memory and processing capabilities, making their deployment and real-time inference both costly and impractical for widespread use.
Quantization has a solution for this. It is a technique to alleviate these challenges by reducing the numerical precision of model parameters and activations. Traditional LLMs utilize 32-bit floating-point representations (FP32) for weights and activations, which, while precise, are resource-intensive. Quantization reduces this precision to 16-bit (FP16), 8-bit (INT8), or even lower bit-widths, effectively compressing the model size and decreasing computational overhead.
However, applying quantization to LLMs is non-trivial due to the inherent sensitivity of these models to precision loss. Direct quantization can lead to significant degradation in model performance, characterized by a decline in accuracy and the introduction of errors in language understanding and generation tasks.
To address these issues, several advanced quantization methodologies have been developed:
Post-Training Quantization (PTQ): This technique involves quantizing a fully trained model without additional retraining. PTQ uses calibration datasets to determine optimal scaling factors and zero-points for quantization, aiming to minimize the impact on model accuracy. Methods like symmetric and asymmetric quantization, per-channel scaling, and weight clustering are employed to enhance performance.
Quantization-Aware Training (QAT): QAT integrates quantization operations into the training process. By simulating low-precision arithmetic during forward and backward passes, the model learns to compensate for quantization errors. This results in weights and activations that are more robust to precision loss, thereby preserving accuracy post-quantization.
Mixed-Precision Quantization: Recognizing that different layers and operations within an LLM have varying sensitivities to quantization, mixed-precision strategies assign different bit-widths to different parts of the model. For instance, attention layers critical for capturing contextual relationships might use higher precision, while less sensitive layers use lower precision.
Adaptive and Dynamic Quantization: These approaches adjust quantization parameters on-the-fly based on the input data or during runtime, optimizing the trade-off between performance and efficiency dynamically.
The implementation of these quantization techniques has yielded quantized LLMs that maintain performance metrics comparable to their full -precision counterparts. For example, models like BERT and GPT variants have been successfully quantized to INT8 with minimal loss in accuracy, enabling faster inference and reduced memory usage.
The benefits of quantization are multifold:
- Reduced Memory Footprint: Lower-precision representations consume less memory, allowing for larger models to fit into limited hardware resources.
- Increased Throughput: Integer operations are generally faster than floating-point operations on modern processors, leading to faster inference times.
- Energy Efficiency: Reduced computational requirements translate to lower energy consumption, which is crucial for battery-powered devices.
Some preview code of how to apply quantization to a LLM can be found below:
def quantization_aware_training(model, train_loader, epochs):
optimizer = optim.Adam(model.parameters(), lr=0.001)
for epoch in range(epochs):
for data, target in train_loader:
optimizer.zero_grad()
# Forward pass with fake quantization
output = model.forward(data)
# Simulate quantization of weights and activations
for layer in model.layers:
# Fake quantize weights
weight = layer.weight
weight_scale = (weight.max() - weight.min()) / (2**8 - 1)
quantized_weight = torch.round(weight / weight_scale) * weight_scale
layer.weight = quantized_weight
# Fake quantize activations
activation = layer.activation
activation_scale = (activation.max() - activation.min()) / (2**8 - 1)
quantized_activation = torch.round(activation / activation_scale) * activation_scale
layer.activation = quantized_activation
loss = loss_function(output, target)
loss.backward()
optimizer.step()
return model
def post_training_quantize(model, calibration_data):
quantized_model = copy.deepcopy(model)
# Step 1: Collect statistics on activations
activation_min = {}
activation_max = {}
for data in calibration_data:
activations = quantized_model.forward(data)
for layer_name, activation in activations.items():
if layer_name not in activation_min:
activation_min[layer_name] = activation.min()
activation_max[layer_name] = activation.max()
else:
activation_min[layer_name] = min(activation_min[layer_name], activation.min())
activation_max[layer_name] = max(activation_max[layer_name], activation.max())
# Step 2: Quantize weights and activations
for layer in quantized_model.layers:
# Quantize weights
weight = layer.weight
weight_scale = (weight.max() - weight.min()) / (2**8 - 1) # For 8-bit quantization
quantized_weight = ((weight / weight_scale).round()).astype(np.int8)
layer.weight = quantized_weight
layer.weight_scale = weight_scale
# Quantize activations using collected statistics
act_min = activation_min[layer.name]
act_max = activation_max[layer.name]
activation_scale = (act_max - act_min) / (2**8 - 1)
layer.activation_scale = activation_scale
return quantized_model
def mixed_precision_quantize(model):
quantized_model = copy.deepcopy(model)
for layer in quantized_model.layers:
if layer.type == 'Attention':
# Use higher precision for sensitive layers
bit_width = 16 # e.g., 16-bit quantization
else:
# Use lower precision for less sensitive layers
bit_width = 8 # e.g., 8-bit quantization
# Quantize weights
weight = layer.weight
weight_scale = (weight.max() - weight.min()) / (2**bit_width - 1)
quantized_weight = ((weight / weight_scale).round()).astype(get_int_type(bit_width))
layer.weight = quantized_weight
layer.weight_scale = weight_scale
# Similarly quantize activations if needed
# ...
return quantized_model
def get_int_type(bit_width):
if bit_width <= 8:
return np.int8
elif bit_width <= 16:
return np.int16
else:
return np.int32
def adaptive_quantization_inference(model, input_data):
# Adjust quantization scales based on input data
activation_min = input_data.min()
activation_max = input_data.max()
activation_scale = (activation_max - activation_min) / (2**8 - 1)
# Quantize input data
quantized_input = ((input_data / activation_scale).round()).astype(np.int8)
# Forward pass with dynamic quantization
output = quantized_input
for layer in model.layers:
# Dynamic adjustment of scales if needed
# Quantize weights and activations on-the-fly
weight = layer.weight
weight_scale = layer.weight_scale # May adjust dynamically
quantized_weight = ((weight / weight_scale).round()).astype(np.int8)
# Compute output
output = quantized_convolution(output, quantized_weight)
# Dequantize if necessary for further processing
output = output * activation_scale # Convert back to higher precision if needed
# Update activation scale for next layer based on current output
activation_scale = (output.max() - output.min()) / (2**8 - 1)
return output