Having fun with decoding and optimization
Hey. One topic very fascinating for me is coding theory. It can be very challenging and it can be pleasing for a more mathematical inclined person or someone like me that, likes a lot mathematics but like engineering as well. I think that the beginning of coding theory is strong related to Shannon work, “A mathematical theory of communication” but it can be interpreted in a very broad sense. What I mean by that is that a lot of natural phenomenum can be interpreted as an application of coding theory. For instance, you can consider the language as a coding theory application where what is done by expressing ourselfs in words is to find an optimal code for communicating thoughts. Other interesting example is what happens in natural evolution. Basically, there you can interpret the changes on environment and the DNA of species being on a communication channel where the DNA is coding the optimal way to survive on a given environment.
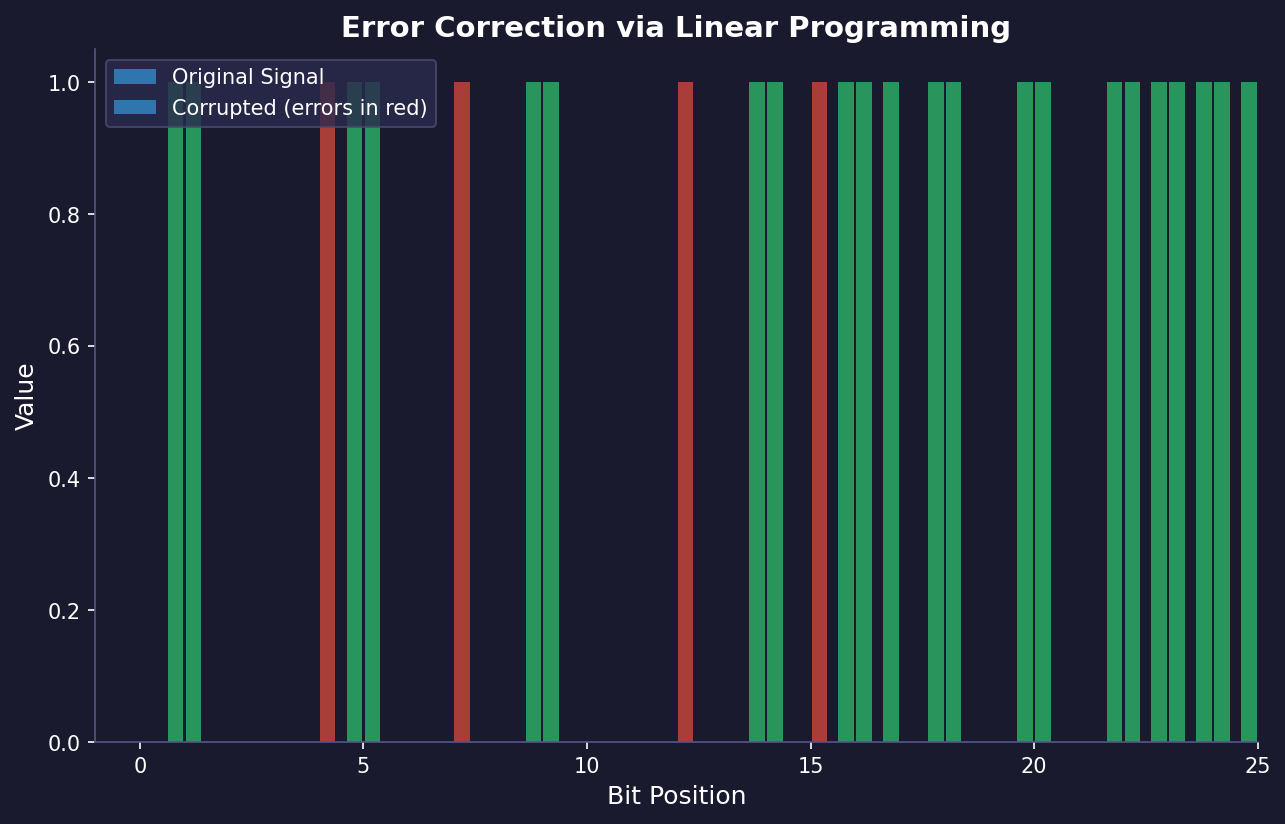
During the years a lot of new approaches having being through of what is the most optimal way of coding and retrieving messages through a communication channel. One interesting topic that appeared recently is how to code messages in a way that a is reliable and secure, and most importantly, can be used in a cryptopgraphic way to resist the attack of quantum computers, but I think that would be more interesting to disccus in another post. On this post i will be focusing on optimal way to retrieve messages corrupted by noise. One very interesting way that I will be implementing here is the way Candes and Tao explored on their famous paper titled Decoding by Linear Programming Paper.
On their words: This paper delves into a traditional issue often discussed in the realm of coding theory, which is the correction of errors. The goal is to accurately retrieve an input vector from corrupted measurements. These measurements are the result of combining the input vector with a specific matrix, and then adding some errors, which are both random and unknown. The central question is whether it’s feasible to precisely reconstruct the original input from these tainted measurements.
Our findings affirm that, given certain conditions related to the matrix used in the process, the original input is the only answer to a particular optimization problem that focuses on minimizing the sum of the absolute values of the components. This is true especially when the number of non-zero elements in the error vector is relatively small, being less than a specific proportion of the matrix’s row count. In essence, the original input can be accurately recovered by solving a straightforward optimization problem, which can also be seen as a type of linear programming.
Moreover, our numerical tests indicate that this method of recovery is exceptionally effective, managing to accurately retrieve the original input even in scenarios where a considerable portion of the measurements is tainted. This research not only addresses the challenge of extracting sparse solutions from systems of linear equations that are significantly underdetermined but also ties closely with the task of reconstructing signals from severely incomplete measurements. In fact, the findings presented in this paper build upon and enhance our previous work. At the heart of this successful approach is a fundamental principle we term the uniform uncertainty principle, which we will explore in detail.
I find this idea very ellegant because it solve fundamental problem in a very simple and efficient way. For more details regarding the mathematical aspects of the idea you can find on the original paper linked above. Here is the implementation and some tests in python of the idea Github Page.